02022020 e il coding palindromo

Oggi è una data palindroma, di quelle che lo sono quasi per tutti, perchè la si può leggere da sinistra a destra o da destra a sinistra sia nella rappresentazione a noi familiare (gg mm aaaa) che in quella anglosassone che mette il mese prima del giorno (mm dd yyyy). Basta pensarci un attimo per accorgersi che è un’eventualità molto rara, che merita qualche riflessione. Del resto questa comunità è sensibile per costruzione alla rappresentazione delle date, perchè ha preso origine da Code’s cool, la piccola comunità fondata l’11-12-13 alle 14:15 per creare un ponte informale tra università e scuola attrverso sessioni di coding in diretta streaming, webinar e mooc ante litteram.

La natura palindroma attiene alle rappresentazioni e non agli oggetti rappresentati.

ASCII

Prendiamo proprio la data di oggi, 02022020, e pensiamo alla sua rappresentazione all’interno del computer o dello smartphone che ce la sta mostrando. Innanzitutto, se i tre elementi che la compongono venissero trattati come giorno, mese e anno, tornerebbero ad essere 2, 2 e 2020, rompendo il palindromo. Ma anche attenendoci alla sequenza di caratteri che vediamo, senza prentendere di interpretarla, ogni carattere, o cifra, ha una propria rappresentazione binaria a 8 bit, secondo il codice ASCII o una delle sue evoluzioni. Lo ‘0‘ è 00110000, il ‘2‘ è 00110010.

Vista come sequenza di bit, la data diventa quindi:

00110000 00110010 00110000 00110010 00110010 00110000 00110010 00110000

Se provassimo a leggerla al contrario risulterebbe diversa e se consultassimo la tabella del codice ASCII per vedere a cosa corrisponderebbe la sequenza di bit invertita otterremmo una stringa non rappresentabile, alternanza di ‘L’ e caratteri speciali che servono a cambiare pagina.

Se di ogni carattere ASCII prendiamo la rappresentazione esadecimale (i cui simboli rappresentano configurazioni di 4 bit alla volta), otteniamo, 3 0 3 2 3 0 3 2 3 2 3 0 3 2 3 0 che non è ancora palindroma.

Pixel art

E cosa possiamo dire dei pixel dello schermo su cui appare la data? Tutto dipende dal tipo e dalla dimensione dei caratteri che decidiamo di utilizzare, ma la natura palindroma della rappresentazione viene di nuovo messa in discussione. Ecco un esempio…

Consideriamo l’immagine riga per riga e codifichiamo con 0 e 1 i quadretti vuoti e pieni. La prima riga, composta da 64 bit, è palindroma (provare per credere). La seconda riga pure. E la terza?… No!

L’intera immagine, di 8 righe, richiede 64×8 = 512 bit. La codifica dell’immagine si ottiene concatenando le sequenze di bit di ogni riga. Nel complesso, è palindroma?

 0 1 1 1 1 1 1 0 0 1 1 1 1 1 1 0 … 0 1 1 1 1 1 1 0

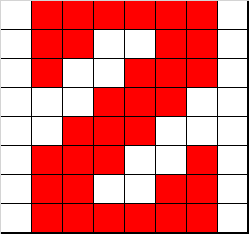
Sì! Ma lo è per il modo fortemente simmetrico in cui ho scelto di rappresentare lo 0 e il 2. Provate a verificare la codifica binaria di questa versione alternativa, con caratteri più tradizionali e meno simmetrici…

E’ ancora palindroma?

Lascio a voi la verifica delle caratteristiche della nuova immagine (azzurra) per tornare alla precedente (rossa), che abbiamo detto avere una codifica binaria palindroma. Se usassimo una rappresentazione esadecimale (per noi decisamente più leggibile) della stessa immagine, cosa otterremmo? Ogni carattere esadecimale codifica 4 pixel, quindi ne abbiamo non più 64, ma solo 16 per riga. Ecco i primi… e gli ultimi:

7 E 7 E … 7 E

Anche senza analizzare tutti i caratteri esadecimali che ho omesso, bastano i primi e gli ultimi per dirci che la rappresentazione non è palindroma.

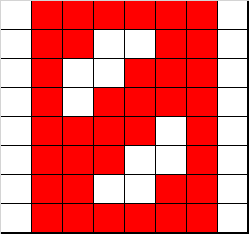
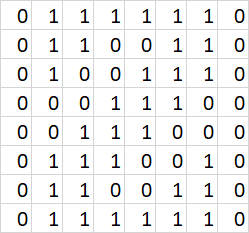
Ora concentriamoci sulla rappresentazione grafica di ogni singola cifra e proviamo a verificare che sia palindroma.

In binario la codifica è la seguente (vedete i bit scritti nella posizione dei corrispondenti pixel, ma dovete immaginarli tutti in sequenza, riga dopo riga):

In esadecimale risulta invece:

7 E  6 6  4 E  5 E  7 A  7 2  6 6  7 E

Se utilizziamo la codifica RLE (Run Lenght Encoding), che in ogni riga specifica il numero di pixel contigui di un dato colore (b per bianco e r per rosso), otteniamo:

Potremmo anche interpretare ogni riga come un byte, parola di 8 bit, a cui attribuire il valore decimale ottenuto considerando che i bit abbiano peso che raddoppia da destra a sinistra (1 il bit più a destra, 128 il bit più a sinistra). Ecco cosa ne sarebbe della nostra immagine:

126 102 78 94 122 114 102 126

Quale di queste rappresentazioni è palindroma?

Avete voglia di fare la stessa verifica per le diverse rappresentazioni del 2?

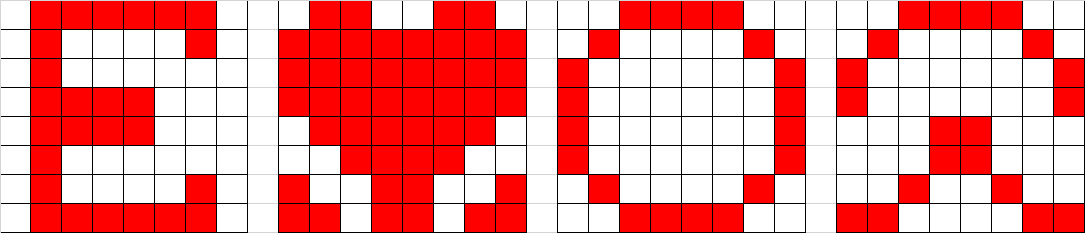
Di seguito propongo qualche altra immagine 8×8 di cui verificare se i diversi tipi di rappresentazioni siano palindrome o no.

Per continuare a giocare con la pixel art esadecimale palindroma e non, potete usare il seguente progetto Scratch

CodyRoby

Ora pensiamo a Roby che si muove su una scacchiera seguendo semplici istruzioni di movimento impartite da Cody: A per avanti, S per sinistra, D per destra. Ogni sequenza di istruzioni è una stringa (sequenza di caratteri) e come tale può essere o non essere palindroma. Che caratteristica hanno i percorsi disegnati seguendo sequenze di istruzioni palindrome?

CodyColor

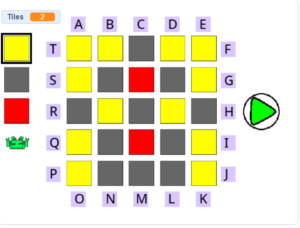
CodyColor rappresenta le istruzioni direttamente lungo il percorso, attraverso mattonelle colorate. Il robot avanza passando da una mattonella all’altra per ricevere nuove istruzioni. Se la mattonella su cui passa è grigia prosegue diritto, se è gialla ruota di 90 gradi a sinistra prima di passare alla mattonella successiva, se è rossa ruota di 90 gradi a destra. La sequenza di istruzioni corrisponde quindi alla sequenza di colori che Roby incontra lungo il percorso e che ne determina il tracciato.

La scacchiera rappresentata in figura contiene un percorso palindromo? Se lo contiene, da dove deve entrare Roby per percorrerlo? Da dove esce? Quante tessere percorre?

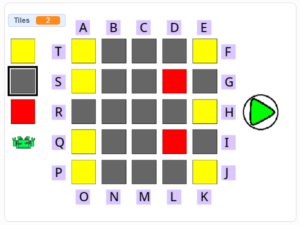
Quella seguente ne contiene?

Potete usare questo progetto Scratch per verificare gli schemi proposti o per creare altri percorsi palindromi. Sono curioso di sapere qual è il più lungo percorso palindromo che si riesce a disegnare su una scacchiera 5×5…