Pixel art e geometria del taxi

La diffusione della pixel art nella scuola, soprattutto nella primaria, ha superato ogni aspettativa (basta sfogliare la raccolta di foto del gruppo Facebook di CodeMOOC per farsene un’idea!). A motivarne il successo credo sia innanzitutto la gratificazione data dalla gradevolezza del risultato grafico e dal piacere di trovare riscontro nei disegni gli uni degli altri, per effetto del rigore metodologico con cui sono stati creati. E’ proprio in virtù di questo rigore che la pixel art rientra di diritto tra le attività di coding unplugged.

Dettati grafici

La scomposizione dell’immagine di pixel ne rende possibile il dettato grafico, che presuppone una convenzione rigorosa tra chi detta e chi esegue il disegno, del tutto analoga alla convenzione tra programmatore ed esecutore tipica del coding. Qualunque sia il repertorio delle istruzioni che si decide di utilizzare per effettuare il dettato grafico, alla base c’è sempre una convenzione implicita, suggerita dalla griglia su cui si effettua il disegno: ogni quadretto va interamente riempito di uno stesso colore. Su questa base si appoggiano convenzioni di diverso tipo utili ad individuare i quadretti da colorare e a stabilirne il colore. Benché nessuno dei disegni fatti a mano dai bambini sia esattamente uguale all’altro per via delle inevitabili imprecisioni e dei diversi strumenti, tutti i disegni appaiono convenzionalmente conformi alla specifica (a meno di errori) per l’interpretazione digitale che siamo portati a darne: vedremo ogni quadretto come pieno o vuoto (senza far caso alle sbavature) e riconosceremo il colore prestabilito (senza far caso alle sfumature). Ci sono pertanto tutti gli elementi utili a fare della pixel art un’attività ricca di spunti didattici legati al pensiero computazionale, alle competenze digitali e al significato stesso di “digitale“.

Questi valori sono presenti, a mio avviso, in tutte le diverse forme nelle quali ho visto proporre attività di pixel art. Ne cito alcune a titolo di esempio, attribuendo dei nomi che spero siano sufficientemente evocativi:

• Run-lenght encoding (RLE). E’ la più immediata e la più diffusa. Accanto ad ogni riga si indicano, partendo da sinistra, le regole di colorazione dei quadretti. Se ci sono quadretti contigui dello stesso colore si indica il colore una sola volta seguito (o preceduto, in base alla convenzione) dal numero di ripetizioni. Ho chiamato questa tecnica RLE perché è il nome che le si dà nel gergo della compressione delle immagini, dove è ampiamente utilizzata.
• Plotter. Si danno le istruzioni di movimento e colorazione come se la mano del disegnatore fosse la punta di un plotter da spostare sulla griglia in modo assoluto (su, giù, destra, sinistra) per arrivare sui quadretti da colorare.
• Cody-roby pixel art. Si posiziona un robot (Roby) in un punto della griglia, indicandone anche l’orientamento assoluto (nord, sud, est, ovest). Quindi Cody (il programmatore) dà istruzioni di movimento a Roby (Vai avanti, Girati a sinistra, Girati a destra). Si può adottare una convenzione in base alla quale Roby colori uniformemente tutte le caselle su cui passa. In questo caso non è necessario esplicitare la colorazione perché il disegno sarà formato dalla traccia di Roby. Se si vogliono usare colori diversi o ammettere spostamenti senza traccia occorre aggiungere istruzioni di colorazione o comandi del tipo PennaSu e PennaGiu.
• Pixel art esadecimale. Si suddivide ogni riga della griglia in segmenti di 4 quadretti (nibble) ai quali è associata un’unica cifra esadecimale che ne esprime le modalità di colorazione. Ogni quadretto è trattato come un bit che può essere pieno (1) o vuoto (0). Secondo la notazione posizionale in base 2, i 4 bit che compongono il nibble hanno pesi pari alle prime 4 potenze di 2, da destra a sinistra: 1, 2, 4, 8. La cifra esadecimale corrisponde alla somma dei pesi dei quadretti da riempire (da 0 a 15).
• Copia. Anche la mera copiatura di un disegno già fatto può offrire spunti di riflessione, in quanto sottintende l’adozione di una strategia algoritmica per portare effettuare la copia. Esplicitare tale strategia può essere un esercizio meno banale del previsto.

Geometria del taxi

Vi propongo di analizzare le forme geometriche che compongono i vostri disegni in pixel art per verificare che godano di una particolare proprietà, detta orto-convessità. Si tratta della trasposizione “debole” del concetto di convessità, proprio della geometria euclidea, in una geometria non euclidea detta “geometria del taxi” di Minkowski. La proprietà è molto più semplice di quanto il nome lasci intendere e può essere spiegata facilmente senza fare riferimento a proprietà geometriche, se ritenute premature.

Una figura è orto-convessa se tra ogni coppia di punti esiste un percorso interno alla figura formato da un solo segmento orizzontale, o da un solo segmento verticale, o da due segmenti orizzontale e verticale.

Su una griglia la proprietà può essere enunciata in modo ancora più semplice ricorrendo al coding. E’ questa la definizione che vi propongo di usare.

Una figura in pixel art è orto-convessa se Roby può andare da ogni quadretto ad ogni altro girando a destra o a sinistra, al più, una volta senza uscire dalla figura.

Ad esempio, la T è orto-convessa, mentre la C non lo è, perché per andare dal punto a al punto b occorre girare a destra due volte.

Vi propongo tre attività da svolgere su carta a quadretti.

1. Disegnare forme orto-convesse che rappresentino ciò che volete (qui la difficoltà sta nel rendere l’idea di ciò che volete rappresentare senza violare la proprietà). Per rendere ludica l’attività, a turno un giocatore fa il disegno scrivendo in un foglietto nascosto cosa intende rappresentare. Gli altri fanno a gara per indovinare e guadagnare punti, ma al tempo stesso verificano l’orto-convessità del disegno.
2. Disegnare una forma arbitraria, suddividendola nel minor numero possibile di zone orto-convesse. La dinamica del gioco può essere la stessa del gioco precedente, ma aumenta la libertà di disegno.
3. Comporre disegni in pixel art formati da zone di colore omogeneo orto-convesse. Stessa dinamica dei giochi precedenti.

Ho provato ad improvvisare un video per proporre queste attività quando mi sono venute in mente, ma eravamo in montagna e il gruppo ci stava lasciando indietro… Non credo che il video sia servito a molto, se non a farvi gli auguri.

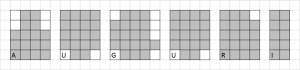
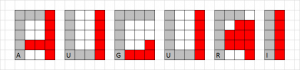
Esempio di alfabeto orto-convesso (sono certo che farete di meglio!)

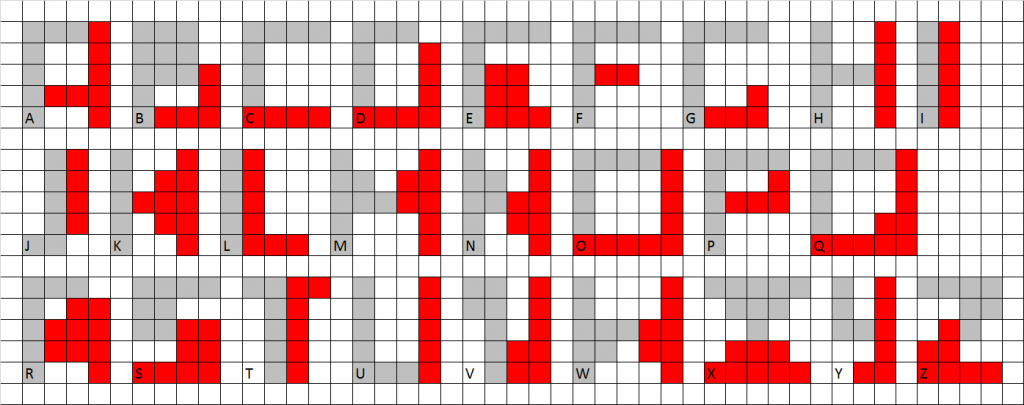
Esempio di alfabeto con caratteri composti da due zone ortoconvesse (anche qui si può fare di meglio!)

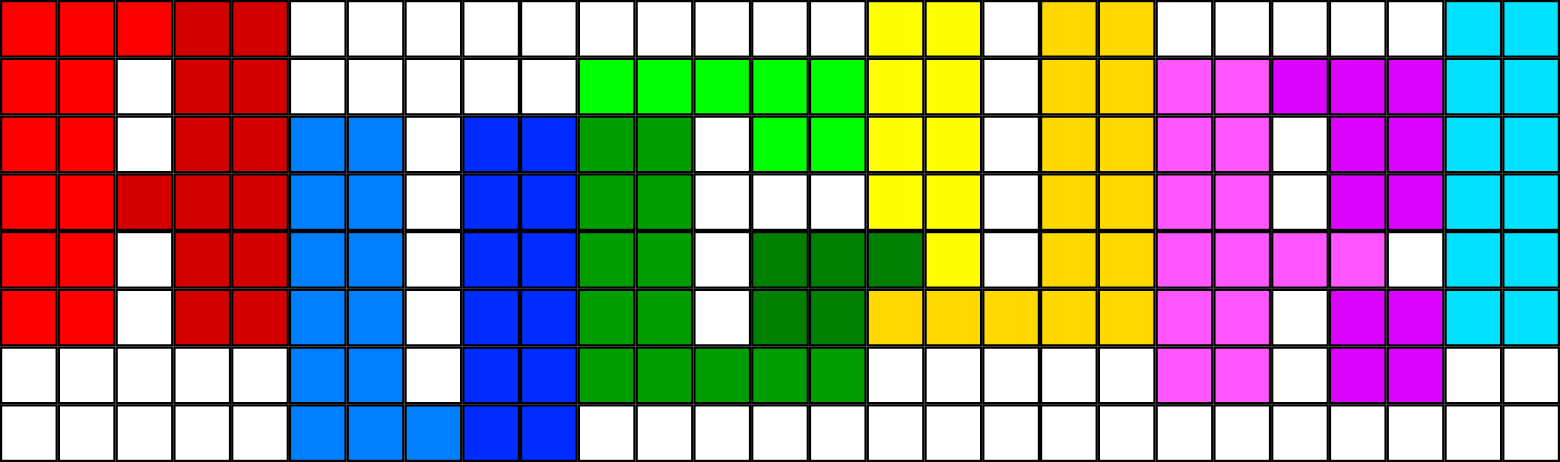
I caratteri della scritta di copertina sono composti da regioni ortoconvesse senza un limite prestabilito al numero di colori.

Calcolo combinatorio

Presi due quadretti, è facile verificare se si possa andare dall’uno all’altro andando sempre dritti e girandosi al più una volta. In altri termini, usando tutte istruzioni Vai avanti con, al più, una sola istruzione di tipo Girati a sinistra o Girati a destra.

Ma per verificare che la figura sia orto-convessa il percorso con una sola curva deve esistere tra ogni coppia di quadretti. Quante verifiche sono necessarie?

Prendiamo ad esempio la figura qui sotto, composta da 5 scacchi. Se ne prendo uno come punto di partenza, ho 4 possibili punti di arrivo. Questo è vero per ogni punto di partenza. Quindi ho 5 possibili punti di partenza e per ognuno di questi 4 possibili destinazioni. Quindi 5×4 coppie di punti. Ma ogni coppia di punti coinvolge due punti e se ho già verificato il percorso dall’uno all’altro non devo anche verificare il percorso inverso, quindi divido per due in numero di verifiche: 5×4/2 = 10.

Se la figura avesse un numero generico di quadretti, diciamo N, le verifiche da fare sarebbero Nx(N-1)/2. nell’ambito del calcolo combinatorio questa formula esprime proprio il numero di combinazioni semplici di N elementi a 2 a 2.

Ma c’è un altro modo per calcolare il numero di verifiche da fare. Torniamo alla nostra figura di 5 quadretti. Potrei partire da uno qualsiasi e verificare i percorsi verso tutti gli altri 4. Dopo averlo fatto metto una crocetta sul punto di partenza già scelto per ricordarmi che non ho più bisogno di considerarlo. A questo punto prendo un altro punto e verifico tutti i percorsi verso gli altri punti, tranne che verso quello con la crocetta, che sono 3. Procedendo così mi restano da fare altre 2 verifiche e poi 1. In totale: 4+3+2+1 = 10, come sapevamo.

In generale, ripetendo il ragionamento per una figura con N quadretti, otterrei (N-1)+(N-2)+…+3+2+1 = Nx(N-1)/2.

In altre parole, la formula che abbiamo ricavato esprime la somma dei primi N-1 numeri interi. Potete facilmente verificarlo scegliendo qualche valore di N, ad esempio 10: 9+8+7+6+5+4+3+2+1 = 10*9/2 = 45. Ma potete anche dimostrarne la validità generale per induzione.

Quindi il numero di verifiche da fare cresce molto in fretta all’aumentare delle dimensioni del disegno. In compenso non appena troviamo un controesempio, una coppia di quadretti tra i quali non esista un percorso rettilineo o ortogonale, sappiamo senza ulteriori verifiche che la figura non è orto-convessa. In pratica è molto più facile confutare la proprietà che verificarla. Per confutare il “per ogni” basta che un “esiste almeno“.

Quest’ultima sezione non è altro che una raccolta non molto ordinata di riflessioni che spero possano offrire spunti per attività didattiche da proporre a diverse età, con o senza riferimento alla pixel art.